Show That the Cdf of a Uniform Continuous Rv is X

Continuous Random Variables

• Probability Distributions

Some differences between discrete and continuous probability distributions:

Discrete Random Variables	Continuous Random Variables
Density functions are nonnegative for all real numbers but greater than zero only at a finite or countably infinite number of points.	Density functions are nonnegative for all real numbers and are greater than zero on certain intervals of real numbers.
The sum of the discrete density function summed over all real numbers is 1.	The integral of the continuous density function integrated over all real numbers is 1.
They may have nonzero probability at some real numbers.	They have zero probability at every real number.
The probability of an event is found by summing the values of the discrete pdf at real numbers defined by event.	The probability of an event is found by integrating the continuous pdf for all real numbers defined by the event.

The next statement shows how to compute the probability that continuous random variable X with pdf f(x) lies in the interval [a,b].

The cumulative density function (cdf) for random variable X with pdf f(x) is defined as follows:

Some of the commonly used continuous random variables are introduced below.  Continuous random variables are introduced by giving either their pdf or cdf.

In dealing with continuous random variables, you may find the resources for graphing and integrating functions on the Mathematical Toolkit page at Vanderbilt University helpful.

---

To Top

• Expected Values

The expected or average value of random variable X with pdf f(x) is given by

and the expected value of the function g(X) of X is computed as

By taking g(x) = x², in the last formula you can find E[X²], and use it in the formula Var[X]=E[X²]-(E[X]²) to find the variance of the random variable X.

---

To Top

• Uniform Random Variable with Parameters a and b

  • Definition

  A Uniform Random Variable with parameters a and b is a continuous random variable that can assume values in any small subinterval of length d within the interval from a to b with equal probability.  The probability is proportional to the length, d, of the interval.

  • Simulation

  Assume that a continuous uniformly distributed random variable, R, on [0,1] can be generated by the computer.  The Uniform RV with parameters a and b can then be simulated by having a computer generate a value of a random variable, R.  Call the value generated r.  Then the value of the uniform random variable, X, with parameters a and b is a + r (b-a).

  A Uniform RV with parameters a and b can also be simulated by a spinner that has values numbered from a to b.

  • Probability Distribution (pdf) and Cumulative Distribution Function (cdf)

  The pdf is denoted by f(x) and the cdf is denoted by F(x).

  

  

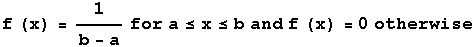
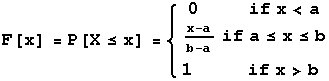
  It is easy to see that f(x) defines a probability density function because it is nonnegative and the integral of the function from -infinity to infinity is 1.

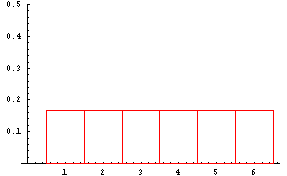
  The next two graphs show the pdf (left graph) and cdf (right graph) of a uniform random variable with parameters 2 and 5.

  

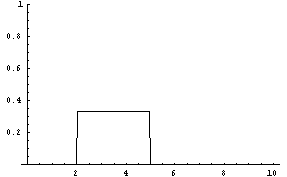
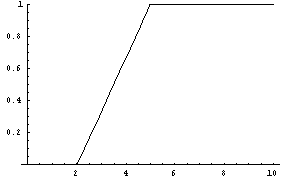
  • Mean and Variance

    • Mean

    

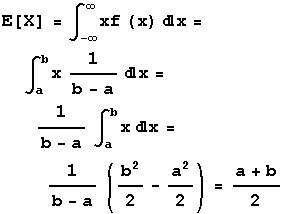
    • Variance

    Var[X]=E[X²]-(E[X]^2.  First E[X²] is found:

    

    Now the formula shown above is applied to find the variance:

    

---

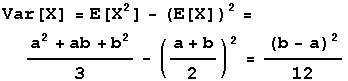
To Top

• Exponential Random Variable with Parameter theta (>0)

  • Definition

  The exponential random variable with parameter theta often gives the waiting time between events.  For example, if customers arrive at a service point according to a Poisson distribution, the time between arrivals has an exponential distribution.  The exponential random variable is also used to model the service time used in servicing customers.  For example, the time needed for a computer to complete a job may be exponentially distributed.

  • Probability Distribution (pdf) and Cumulative Distribution Function (cdf)

  The pdf and cdf for an exponential with parameter theta are shown next.  The pdf is denoted by f(x) and the cdf is denoted by F(x).

  

  

  
  

  Graphs of the pdf (left) and cdf (right) for an exponential RV with parameter 1 are shown next.

  

  • Simulation

  Simulation of a continuous random variable, X, can be carried out by finding the inverse of the cumulative distribution function (cdf) for X.  A result that will not be justified here says that if X has cdf F with inverse function F^-1, then random variable X can be simulated by generating values of a continuous uniform random variable R on [0,1] and finding F^-1[R].  The values F^-1[R] provide a simulated values of X.  This method is limited to continuous random variables for which a closed-form expression for F^-1 can be found.

  In the case of the exponential F^-1[R] = theta(-ln(1-R)).

  • Mean and Variance

    • Gamma Function

    The gamma function is defined by the following improper integral.

    

    This integral has the property that

    

    and this can be used to show that for any positive integer, n,

    

    By making the substitution x =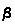y and dx = 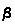dy in the first integral of the following display, you get the identity shown next.

    

    These gamma function identities are used to find the mean and variance of the exponential distribution

    • Mean

    

    • Variance

    

    But Var[X]=E[X²]-(E[X]²) so

    

---

To Top

• Normal Random Variable with Parameters mu ( 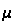) and sigma ( )

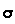  • Definition and Simulation

  The Normal Random Variable is defined by the probability density function shown in the next section.  As you will see the normal random variable has a 'bell-shaped' pdf.  This 'bell-shaped' density function is centered at the mean 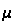and has variability given by standard deviation .

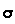  • Probability Distribution (pdf) and Cumulative Distribution Function (cdf)

  The formula for the pdf is shown next.

  

  In the normal pdf x can be any real number.

  The cdf for the normal distribution has no closed-form expression.  It can be expressed as the integral of the pdf from -infinity to x.  There are tables of the cdf (see the back of your textbook) for the special case 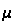=0 and 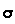=1.  This special case RV is called the Standard Normal Random Variable.  Once you know the cdf for the standard normal RV, you can find the probabilities for any other normal RV by using a z-score formula.  The next display shows the pdf (left graph) and cdf (right graph) for the Standard Normal RV.
  

  
  

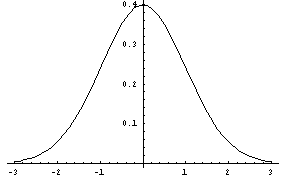
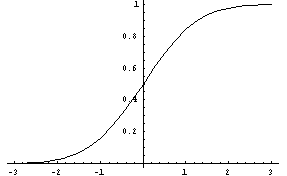
  • Mean and Variance

    The mean and variance computations are shown for the Standard Normal RV.  This special normal random variable is denoted by Z.

    • Mean

    

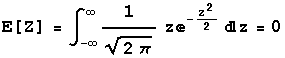
    This integral is zero because the function is an odd function.

    • Variance

    

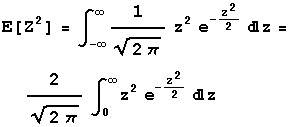
    The integral identity follows because the function being integrated is an even function.  Make the change of variable u = z² so du = 2zdz.  The last integral above then becomes

    

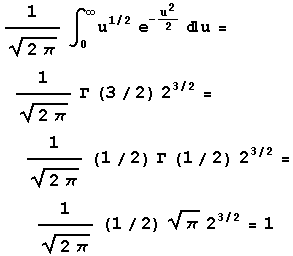
    The last line follows because the gamma function evaluated at 1/2 is the square root of pi.

    Since the mean of the Standard Normal RV is 0, Var[Z] = E[Z²]-(E[Z]²) = 1-0 = 1.

---

To Top

fortuneabling.blogspot.com

Source: https://www.csus.edu/indiv/j/jgehrman/courses/stat50/continuousrvs/5continuousrvs.htm

Share this post